단순히 1개의 원소만 다루는 경우
List 자료구조의 구현 방식에는 각 요소를 포인터와 같은 방법으로 이어 구현하는 LinkedList와 배열을 이용하는 ArrayList가 있다. 각 구현 방식에 따라 다음과 같은 특성을 가진다고 알려져있다.
LinkedList | ArrayList | |
임의 위치 삽입 | O(n) | O(1) |
임의 위치 삭제 | O(n) | O(n) |
임의 위치 접근 | O(n) | O(1) |
그런데, ArrayList의 경우 배열의 크기를 고려해야 한다. ArrayList가 사용하는 배열이 가득 찬 경우 배열을 다시 생성하고, 기존의 배열의 원소를 모두 새로운 배열로 옮겨야 한다. 이것이 고려되어야 하는 상황 즉, n개의 원소를 비어있는 리스트에 순차적으로 삽입하는 상황에서, 시간 복잡도를 다시 생각해 볼 필요가 있다.
n개의 원소를 순차적으로 다루는 경우
LinkedList의 경우, n개의 원소를 리스트의 마지막에 순차적으로 추가하는 경우 시간복잡도가 O(n)이다. 각 삽입에서 이미 마지막 원소의 주소를 알고 있기 때문.
ArrayList의 경우, n개의 원소를 리스트에 추가하는 과정에서 배열을 재할당하는 과정이 없다면 O(n)이지만, 재할당하는 과정이 있다면 O(n)이 아닐 수 있다.
 재할당을 고정 크기 만큼 하는 경우
재할당을 고정 크기 만큼 하는 경우
배열이 가득 찬 경우, 기존 배열의 크기에 고정된 값 R 만큼 늘린 배열을 할당하는 방식이다.
시간 복잡도
최초 배열의 크기를 A 라 하면 재할당하는 횟수 T 는 다음과 같다.
⌈ ⌉ 기호는 올림을 의미한다.
최초 재 할당 시 A개의 원소가 이동한다. 이후 할당 할 때 마다 이전의 재 할당에서 이동한 원소의 개수보다 R개 더 많은 원소가 이동한다. 따라서, 총 이동 횟수는 초항이 A이고, 등차가 R인 등차수열의 T번째 원소까지의 합 만큼 수행된다. 등차수열의 합 공식을 적용하면,
가 되고, 이 식은 n에 대한 2차식이므로 재할당에 필요한 시간 복잡도는 O(n²)이 된다.
n 개의 원소를 순차 삽입하는데 O(n²)의 시간 복잡도가 필요하다.
공간 복잡도
할당되는 메모리의 크기를 고려하는 공간 복잡도의 경우, 모든 원소가 삽입된 시점에 리스트의 크기는 n + R 이하이므로 O(n)의 메모리가 필요하다.
최종적으로 n 개의 원소를 순차 삽입하는데 O(n²)의 시간 복잡도, O(n)의 공간 복잡도가 필요하다.
 재할당을 일정 비율로 하는 경우
재할당을 일정 비율로 하는 경우
배열이 가득 찬 경우, 기존 배열의 크기의 R배 의 배열을 할당하는 방식이다.
시간 복잡도
최초 배열의 크기를 A 라 하면 재 할당 하는 횟수 T 는 다음과 같다.
최초 재 할당 시 A개의 원소가 이동한다. 이 후 재 할당 때 마다 이전의 재할당에서 이동한 원소보다 R배 많은 원소가 이동한다. 따라서 초항이 A이고, 등비가 R인 등비수열의 T번째 항까지의 합 만큼 수행된다. 등비 수열 합 공식과 지수와 로그의 성질을 이용하면
위 두 공식에 의해
즉, N에 대한 1차식이 되어 재할당에 필요한 시간복잡도는 O(n)이 된다.
최종적으로 n 개의 원소를 순차 삽입하는데 O(n)의 시간 복잡도가 필요하다.
공간 복잡도
할당되는 메모리의 크기를 고려하는 공간 복잡도의 경우, 모든 원소가 삽입된 시점에 리스트의 크기는 R * N 이하이므로 O(n)의 메모리가 필요하다.
최종적으로 n 개의 원소를 순차 삽입하는데 O(n)의 시간 복잡도, O(n)의 공간 복잡도가 필요하다.
 결론
결론
일정한 비율로 크기를 늘려 재할당 하는 것이 시간 복잡도 측면에서 더 유리하다.
Java의 ArrayList
Java 17 기준! 물론, 이게 변할 거라고 생각하지는 않지만, 그래도 버전을 명시해야 할 것 같다.
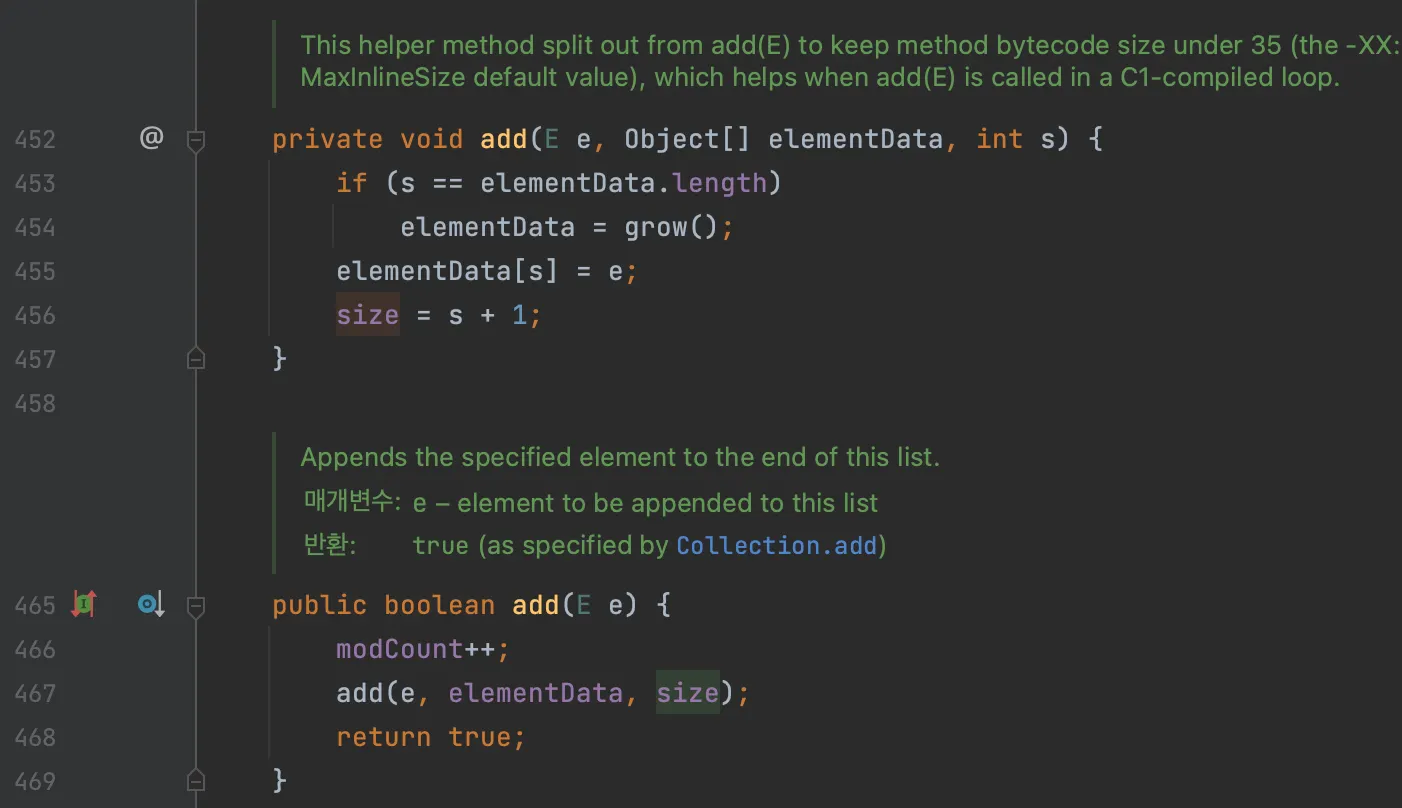
add 메서드
454 번째 라인을 보면, 리스트의 크기가 꽉 찼을 때, grow() 메서드를 호출한다. 이름에서 배열의 크기를 늘리는 메서드임을 추측할 수 있다.
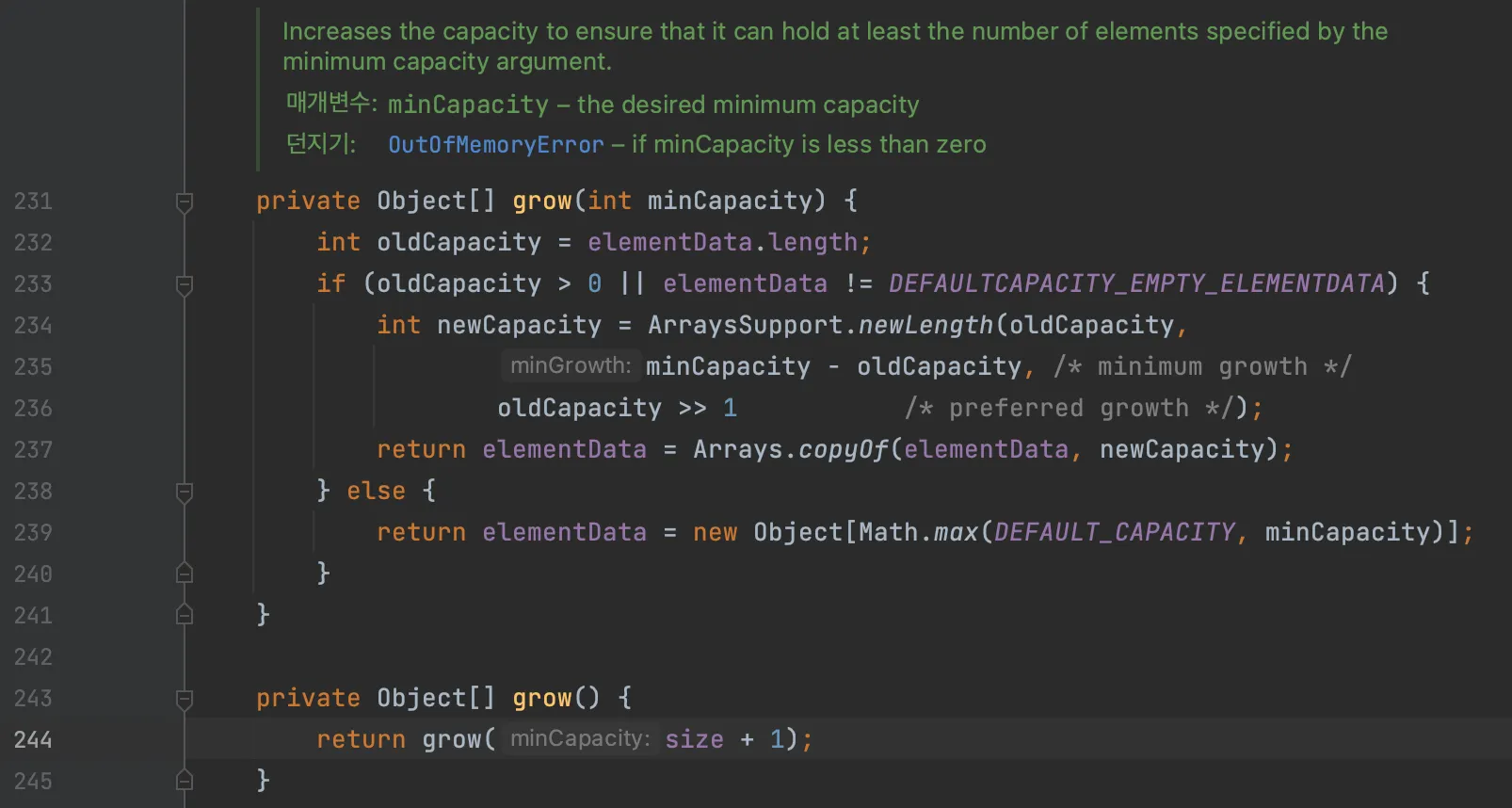
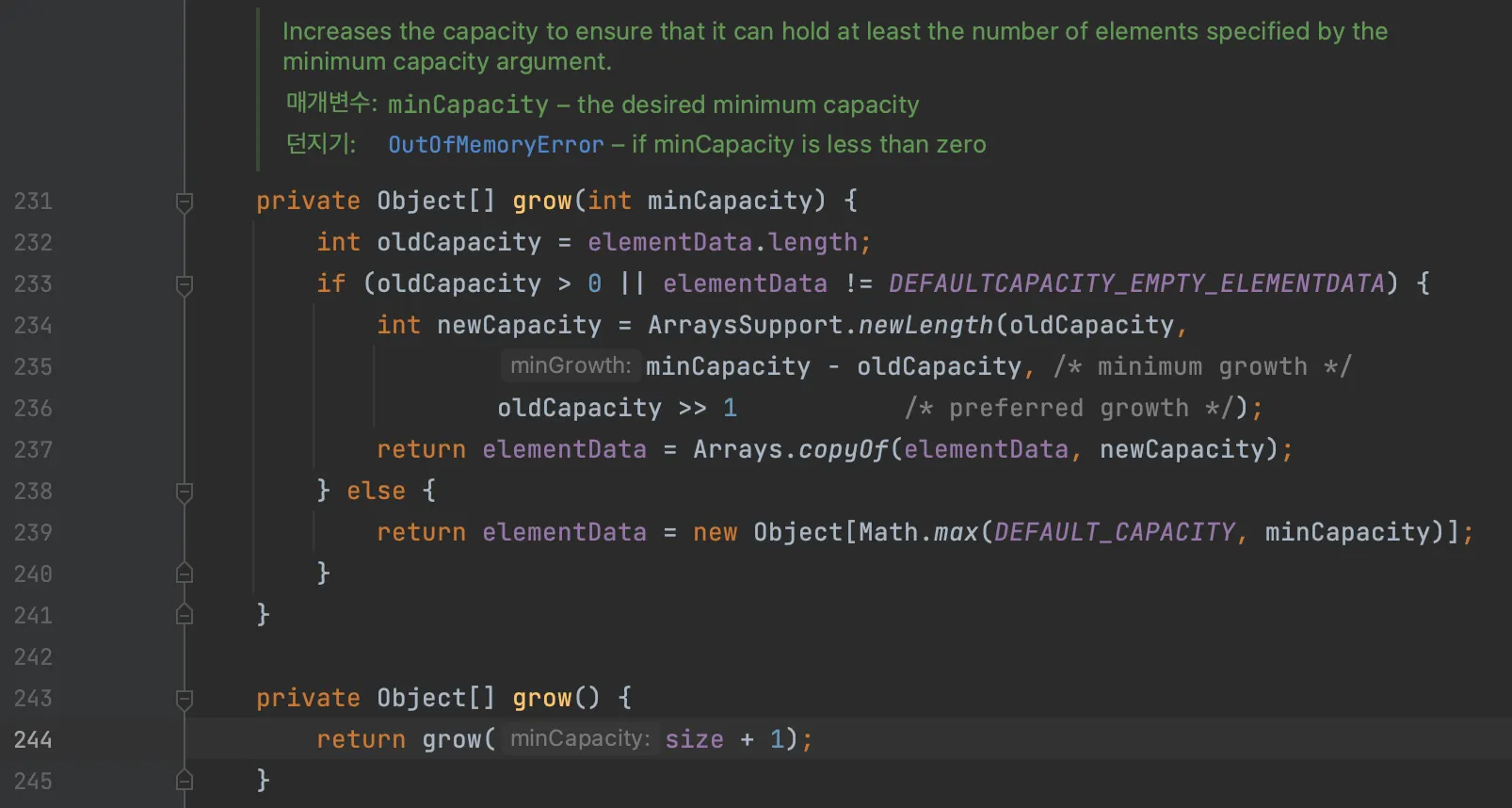
grow 메서드
현재 배열의 크기가 0보다 크거나, 최초의 비어있는 기본 배열이 아닌 경우 ArraysSupport.newLength 메서드를 호출한다.
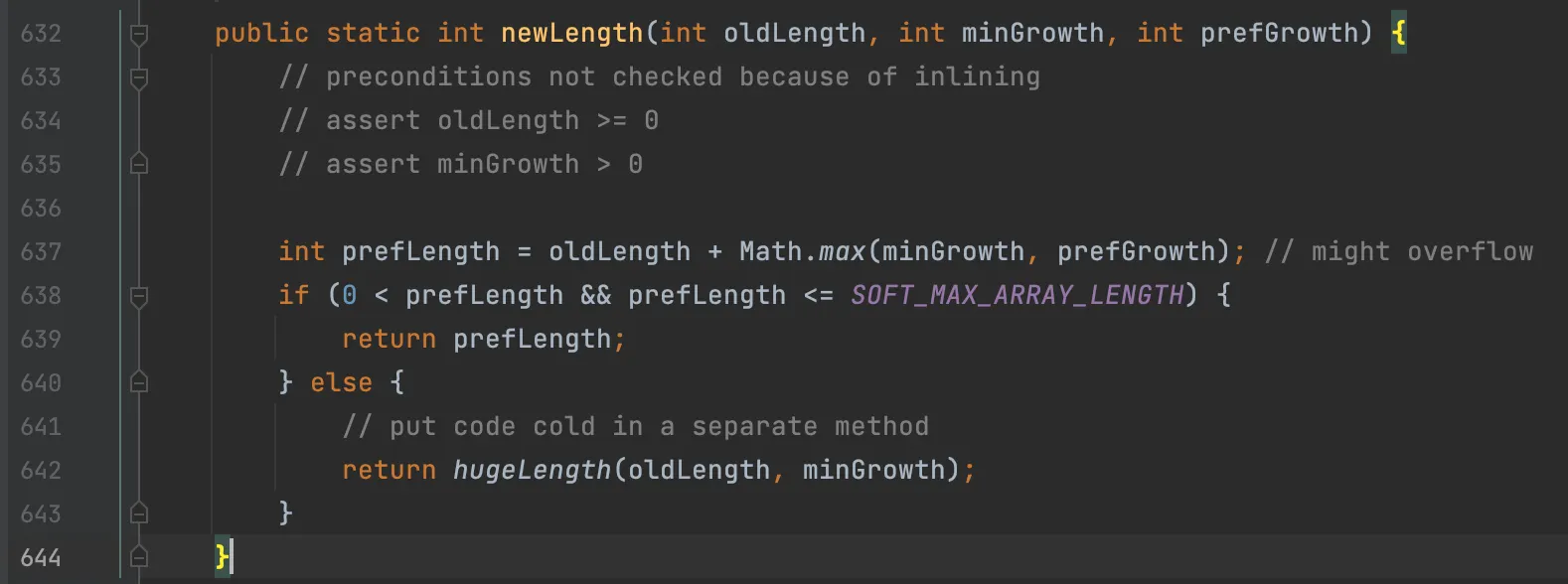
ArraysSupport.newLength(int oldLength, int minGrowth, int prefGrowth) 메서드
기존 크기와 “최소 증가 크기”와 “기대 증가 크기” 중 더 큰 값을 반환한다. if문으로 검사하는 것은 int 범위의 오버플로우를 방지하는 코드다.
235 ~ 236번째 줄을 보면, minCapacity - oldCapacity 가 “최소 증가 크기”이고, oldCapacity >> 1 가 “기대 증가 크기” 임을 알 수 있다. oldCapacity >> 1 는 우측 비트 시프트 연산자를 통해 oldCapacity를 2로 나눈 몫을 계산한 것이다. 즉, 0.5배 한 것 이다.
Java 17 에선 ArrayList가 가득 찬 경우 0.5배씩 내부 배열의 크기를 늘린다.